투포인터 알고리즘(Two Pointers Algorithm)
- 1차원 배열에서 두 개의 점 위치를 기록하면서 원하는 것을 처리하는 알고리즘
- 병합정렬(merge sort)의 기초
- 구간합을 구할 때 매우 유용 (완전 탐색으로 시간초과가 난다면 투포인터를 써보자!)
두 포인터를 보통 start, end 포인터라고 하며, 부분 배열의 처음과 끝을 가르키는 역할을 한다.
맨 처음은 항상 start = end = 0 이며, start 포인터는 end 포인터보다 뒤에 있을 수 없다. (start <= end)
1. 현재 부분합이 M 이상이거나, 이미 배열의 마지막칸에 있다면 start 포인터를 한 칸 앞으로 옮긴다 ( 이 방향 →)
2. M 보다 작다면 end 포인터를 한 칸 앞으로 옮긴다 ( 이 방향 →)
3. 현재 부분합이 M 이라면 count + 1
위의 과정을 start 포인터가 배열의 끝에 도달할 때까지 반복한다.
예제로 특정한 합을 가지는 부분 연속 수열 찾기를 풀면서 설명해보도록 하겠다.
(예제 풀어보기: 수들의 합2)
- N: 배열의 수의 갯수
- M: 부분합이 M 인 것을 구함
-> N칸의 1차원 배열이 있을 때, 부분합이 M인 것을 구하는 예제
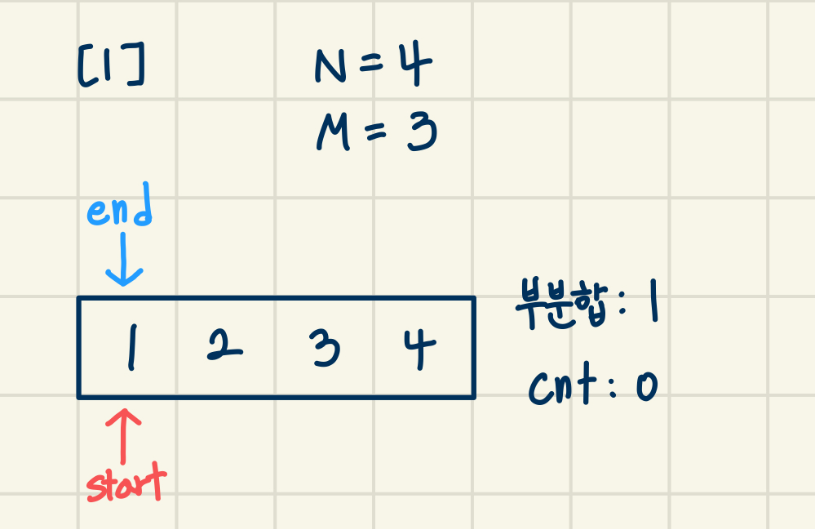
[1]
현재 부분합이 M 보다 작음 -> end + 1
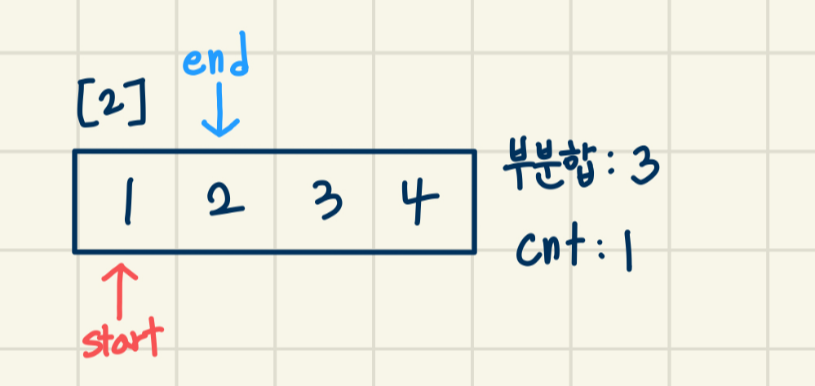
[2]
현재 부분합이 M 과 같음 -> start + 1
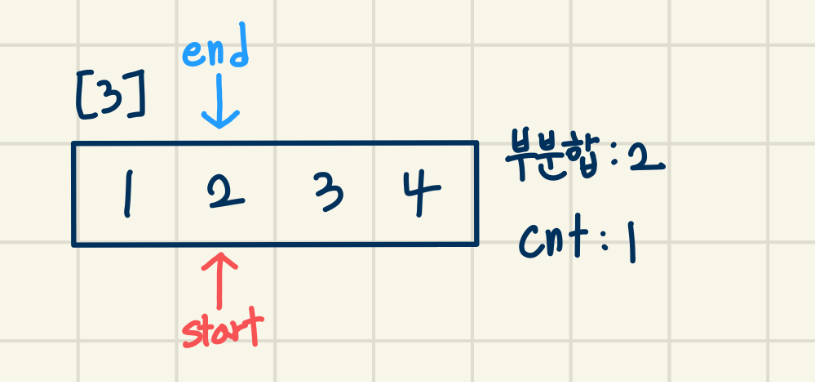
[3]
현재 부분합이 M 보다 작음 -> end + 1
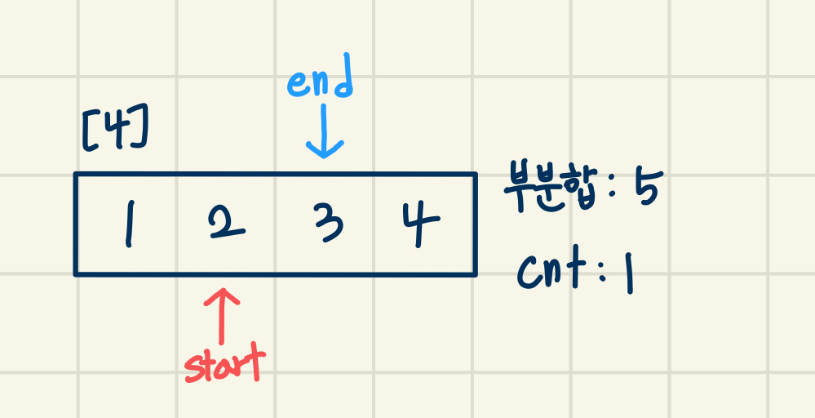
[4]
현재 부분합이 M 보다 큼 -> start + 1
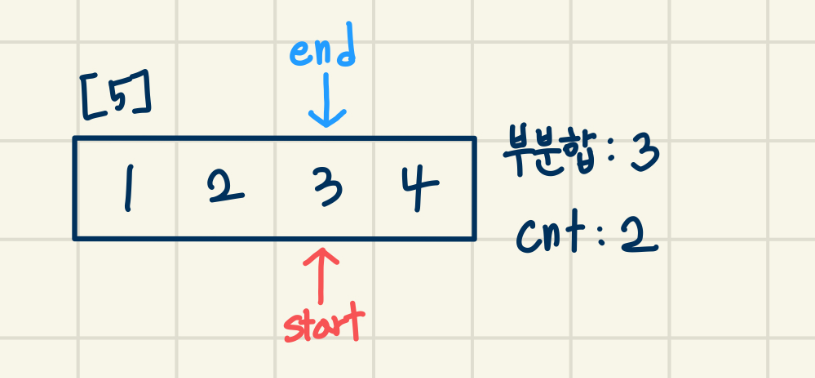
[5]
현재 부분합이 M 과 같음 -> start + 1
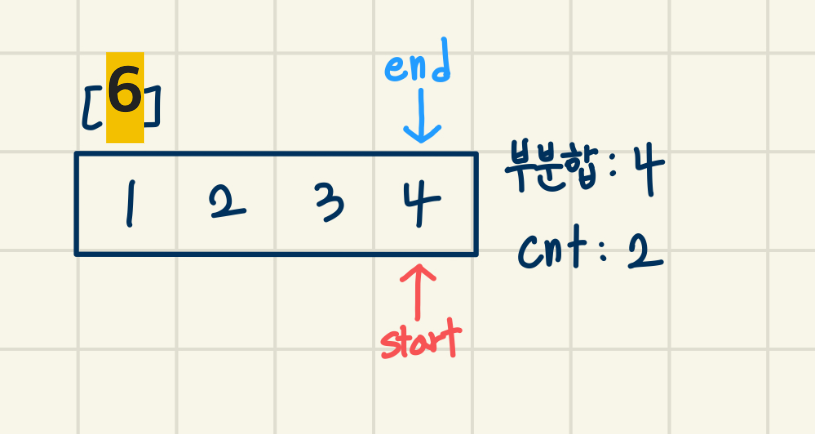
[6]
배열의 끝까지 갔으니 끝
코드
N = 4 # 배열의 숫자 갯수 N
M = 3 # 구하려는 부분 합 M
cnt = 0
S = 0
end = 0
for start in range(n):
while S < M and end < N:
S += arr[end]
end += 1
# 부분합이 M일 때 카운트 증가
if S == M:
cnt += 1
S -= arr[start]
print(cnt)
위 코드의 시간 복잡도는 O(N) 이다.
for 문 안에 while 문이 있는데 어떻게 O(N) 이라고 생각할 수 있는데 찬찬히 생각해보자.
-> 이 알고리즘은 매 루프마다 항상 두 포인터 중 하나는 1씩 증가하고 있고, 각 포인터가 N 번 누적 증가해야 알고리즘이 끝이 난다.
따라서 각각 배열의 끝에 다다르는데 O(N) 이라 O(N+N) = O(N) 이므로 결국 O(N) 이 되는 것!
References
https://m.blog.naver.com/kks227/220795165570
투 포인터(Two Pointers Algorithm), 슬라이딩 윈도우(Sliding Window) (수정: 2019-09-09)
조금 성향이 비슷하다고 생각하는 기법 2개를 함께 쓰려 합니다. 첫 번째로 소개해드릴 기법은 투 포인터(t...
blog.naver.com
'Algorithm' 카테고리의 다른 글
| [알고리즘] 이진 탐색(Binary Search) (0) | 2024.08.18 |
|---|---|
| [Algorithm/알고리즘] 누적합 알고리즘 Prefix Sum (0) | 2024.07.09 |
| 스택(stack), 큐(queue) (0) | 2024.01.10 |

